HashMap实现原理

HashMap是Java中比较常用的集合类，它的实现原理也是面试中经常被问到的问题。在JDK8中，HashMap的实现和JDK7中是不一样的，主要有两方面的改进：

• 数据结构：由原来的数组+链表变更为数组+链表+红黑树。
• 寻址优化：JDK7 中通过对 key 值Hash取模的方式定位 value 在数组中的下标位置，JDK8中对hash值的计算发生了变化。

顾名思义，HashMap是一种基于哈希表的Map接口实现。根据HashMap类的注释可以获得几个关键信息：

• 它和Hashtable基本一样，区别在于HashMap不是同步容器，并且允许null作为value和key。
• HashMap是无序的。
• 有两个参数会影响HashMap的性能：initial capacity，初始容量，默认值16；load factor，加载因子，默认值0.75。
• 线程不安全，如果多个线程并发访问一个HashMap，并且至少有一个线程在结构上修改了HashMap，则必须进行外部同步。（结构修改是指添加或删除一个或多个映射的任何操作；仅更改与HashMap已包含的键关联的值不是结构性修改）。

哈希表

将对象转为有限范围的正整数的表示方法，就叫作 Hash，翻译过来叫散列，也可以直接音译为哈希。将对象进行 Hash，用得到的 Hash 值作为数组下标，将对应元素存在数组中。这个数组就叫作哈希表。这样我们就可以利用数组的随机访问特性，达到 O(1) 级别的查询性能。
在HashMap中，这个数组也就是哈希表就是HashMap类的字段，需要注意，数组是在第一次使用的时候才进行初始化的：

/**
 * The table, initialized on first use, and resized as
 * necessary. When allocated, length is always a power of two.
 * (We also tolerate length zero in some operations to allow
 * bootstrapping mechanics that are currently not needed.)
 */
transient Node<K,V>[] table;

而数组中的元素自然就是：

/**
 * Basic hash bin node, used for most entries.  (See below for
 * TreeNode subclass, and in LinkedHashMap for its Entry subclass.)
 */
static class Node<K,V> implements Map.Entry<K,V> {
    final int hash;
    final K key;
    V value;
    Node<K,V> next;
}

然而，任何 Hash 函数都有可能造成对象不同，但 Hash 值相同的冲突。而且，数组空间是有限的，只要被 Hash 的元素个数大于数组上限，就一定会产生冲突。因为数组空间不可能无限增大，再理想的 Hash 函数也无法避免冲突的发生，因此需要在冲突发生时提供存储和查询的方案，常用的有两种：“开放寻址法”和“链表法”。

开放寻址法

开放寻址法是指在冲突发生后，最新的元素需要寻找新空闲的数组位置完成插入。

线性探查

在当前位置发现有冲突以后，就顺序去查看数组的下一个位置，看看是否空闲。如果有空闲，就插入；如果不是空闲，再顺序去看下一个位置，直到找到空闲位置插入为止。查找的逻辑与插入的逻辑一样。
不难发现，哈希表越满的时候，搜索空位置的时间复杂度就越高，因此，线性探查会影响哈希表的整体性能，而不只是Hash值冲突的Key。

二次探查 & 双散列

二次探查就是将线性探查的步长从 i 改为 i^2。第一次探查，位置为 Hash(key) + 1^2；第二次探查，位置为 Hash(key) +2^2，依此类推。
双散列就是使用多个 Hash 函数来求下标位置，当第一个 Hash 函数求出来的位置冲突时，启用第二个 Hash 函数，算出第二次探查的位置，依此类推。
两者的核心思路其实都是在发生冲突的情况下，将下个位置尽可能地岔开，让数据尽可能地随机分散存储，来降低对不相干 Key 的干扰，从而提高整体的检索效率。

缺点

开放寻址法的缺点是当哈希表快满了的时候插入和检索的性能会下降的厉害，而且一旦哈希表满了就需要re-hash，会造成非常大的开销，因此不适合数据动态变化的场景。
此外，使用开放寻址法在删除元素的时候不能直接删除，而是需要设置标志位。在C语言的哈希表实现khash.h使用的就是开放寻址法，但是JDK8的HashMap并不是。

链表法

链表法是指在数组中不存储一个具体元素，而是存储一个链表头。如果一个 Key 经过 Hash 函数计算，得到了对应的数组下标，那么就将它加入该位置所存的链表的尾部。链表法结合了数组和链表，既利用了数组的随机访问特性，又利用了链表的动态修改特性，同时提供了快速查询和动态修改的能力。但是，如果链表很长，遍历代价还是会很高。在JDK8的HashMap实现中，会在链表长度超过8的时候转变为红黑树，在长度小于6的时候再退化回链表。

哈希表的缺点

哈希表接近 O(1) 的检索效率是有前提条件的，就是哈希表要足够大和有足够的空闲位置，否则就会非常容易发生冲突。如果频繁发生冲突，大部分的数据会被持续地添加到链表或二叉检索树中，检索也会发生在链表或者二叉检索树中，这样检索效率就会退化。这也就是上面所说的初始容量和加载因子对HashMap性能的影响很大的原因。

源码分析

put()

public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}

put方法中调用了两个方法：putVal()和hash()。

putVal()

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
    Node<K,V>[] tab; Node<K,V> p; int n, i;
    if ((tab = table) == null || (n = tab.length) == 0)
        n = (tab = resize()).length;
    // 注意此处的寻址方法
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);
    else {
        Node<K,V> e; K k;
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            e = p;
        else if (p instanceof TreeNode)
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
        else {
            for (int binCount = 0; ; ++binCount) {
                if ((e = p.next) == null) {
                    p.next = newNode(hash, key, value, null);
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                        treeifyBin(tab, hash);
                    break;
                }
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e;
            }
        }
        if (e != null) { // existing mapping for key
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e);
            return oldValue;
        }
    }
    ++modCount;
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict);
    return null;
}

这里注意代码的第7行，tab[i = (n - 1) & hash]，这一行其实是用key的hash值对哈希表长度取模从而确定元素在哈希表上的位置。但是这里明明是与运算（两者同为1时，结果才为1，否则为0）为什么说是取模呢？对于现代的处理器来说，除法和求余数（模运算）是最慢的动作。根据公式
$$h \mod 2^n = h \& (2^n - 1)$$
可以使用与运算代替取模运算，从而提高计算性能。上述公式也就解释了为什么哈希表的长度总是2的指数幂了。
整个流程如图：

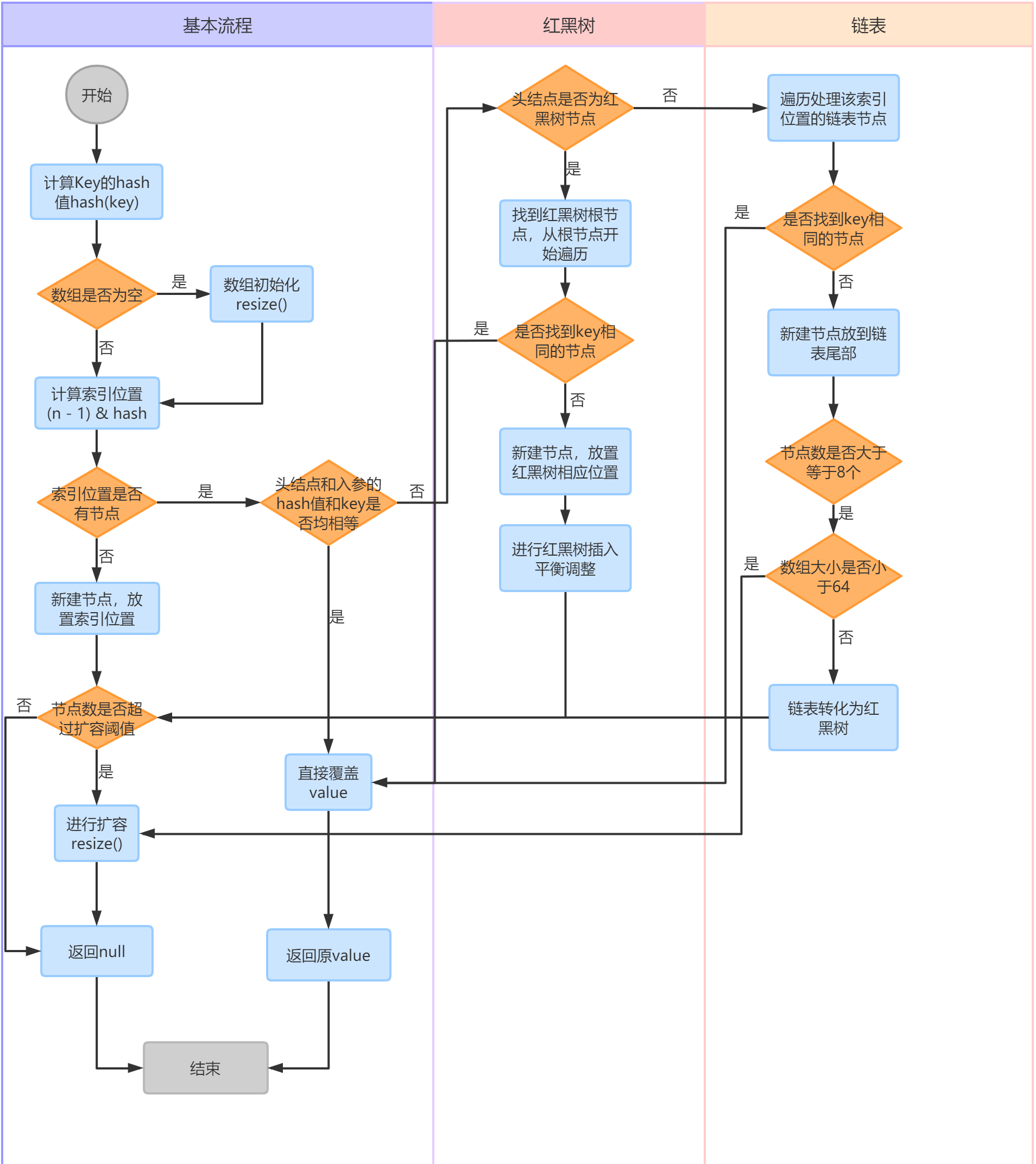
hash()

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

这个方法就是JDK8对寻址的优化了，将hash值的高16位和低16位做异或运算（两者相同为1，不同为0）。为什么这么做呢？源码注释里也有解释：因为哈希表使用2的指数幂作为掩码与hash值做与运算进行寻址。这样无论两个hash值的高位多么的不一样，但是只要最后几位是一样的，那么它们计算出来的值就是一样的，从而发生hash冲突。

所以，JDK8将hash值的高16位和低16位做异或运算，从而将高16位的影响向下传播（spreads the impact of higher bits downward），从而让异或运算结果的低16位融合了原hash值的高16位和低16位的联合特征，这样可以降低哈希冲突从而在一定程度上保证了数据的均匀分布。

get()

public V get(Object key) {
    Node<K,V> e;
    return (e = getNode(hash(key), key)) == null ? null : e.value;
}

final Node<K,V> getNode(int hash, Object key) {
    Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
    // 如果哈希表为空就返回null
    if ((tab = table) != null && (n = tab.length) > 0 &&
        (first = tab[(n - 1) & hash]) != null) {
        // 通过hash值寻址，如果在哈希表上就直接返回
        if (first.hash == hash && // always check first node
            ((k = first.key) == key || (key != null && key.equals(k))))
            return first;
        // 如果不在并且存在链表或者红黑树
        if ((e = first.next) != null) {
            // 如果是红黑树node，那么使用红黑树的检索方法
            if (first instanceof TreeNode)
                return ((TreeNode<K,V>)first).getTreeNode(hash, key);
            // 如果是链表，遍历
            do {
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    return e;
            } while ((e = e.next) != null);
        }
    }
    return null;
}

get方法的逻辑很简单，直接看注释就好了。

resize()

先看源代码的注释：

Initializes or doubles table size. If null, allocates in accord with initial capacity target held in field threshold. Otherwise, because we are using power-of-two expansion, the elements from each bin must either stay at same index, or move with a power of two offset in the new table.

注释说明resize方法用来初始化或者将哈希表的长度变为原来的2倍，也就是扩容逻辑。

final Node<K,V>[] resize() {
    Node<K,V>[] oldTab = table;
    int oldCap = (oldTab == null) ? 0 : oldTab.length;
    int oldThr = threshold;
    int newCap, newThr = 0;
    if (oldCap > 0) {
        if (oldCap >= MAXIMUM_CAPACITY) {
            threshold = Integer.MAX_VALUE;
            return oldTab;
        }
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                 oldCap >= DEFAULT_INITIAL_CAPACITY)
            newThr = oldThr << 1; // double threshold
    }
    else if (oldThr > 0) // initial capacity was placed in threshold
        newCap = oldThr;
    else {               // zero initial threshold signifies using defaults
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
    if (newThr == 0) {
        float ft = (float)newCap * loadFactor;
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                  (int)ft : Integer.MAX_VALUE);
    }
    threshold = newThr;
    @SuppressWarnings({"rawtypes","unchecked"})
    Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
    table = newTab;
    if (oldTab != null) {
        for (int j = 0; j < oldCap; ++j) {
            Node<K,V> e;
            if ((e = oldTab[j]) != null) {
                oldTab[j] = null;
                if (e.next == null) // 普通元素
                    newTab[e.hash & (newCap - 1)] = e;
                else if (e instanceof TreeNode) // 红黑树
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                else { // preserve order 链表
                    Node<K,V> loHead = null, loTail = null;
                    Node<K,V> hiHead = null, hiTail = null;
                    Node<K,V> next;
                    do {
                        next = e.next;
                        if ((e.hash & oldCap) == 0) {
                            if (loTail == null)
                                loHead = e;
                            else
                                loTail.next = e;
                            loTail = e;
                        }
                        else {
                            if (hiTail == null)
                                hiHead = e;
                            else
                                hiTail.next = e;
                            hiTail = e;
                        }
                    } while ((e = next) != null);
                    if (loTail != null) {
                        loTail.next = null;
                        newTab[j] = loHead;
                    }
                    if (hiTail != null) {
                        hiTail.next = null;
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    return newTab;
}

resize方法大致分为两步：确定扩容后哈希表的容量newCap和扩容阈值newThr；元素迁移。

确定容量和阈值

1. 如果扩容前哈希表的容量大于0，判断容量是否超过最大容量值（2³⁰）：如果超过则将阈值设置为Integer.MAX_VALUE也就是2³¹-1，并直接返回扩容前哈希表，不进行扩容操作，因为此时oldCap * 2比Integer.MAX_VALUE大，因此无法进行重新分布，只是单纯的将阈值扩容到最大；如果容量 * 2小于最大容量并且不小于默认初始容量（16），则将容量和阈值设置为原来的两倍。
2. 如果扩容前哈希表的容量为0并且阈值大于0（这种情况发生在新创建的HashMap第一次put时，该HashMap初始化的时候传了初始容量，由于HashMap并没有capacity变量来存放容量值，因此传进来的初始容量是存放在threshold变量上（查看HashMap(int initialCapacity, float loadFactor)方法），因此扩容前哈希表的threshold就是我们要新创建的HashMap的capacity，所以将扩容后哈希表的容量设置为扩容前的阈值。
3. 如果扩容前哈希表的容量为0并且阈值为0，这种情况是没有传容量的new方法创建的空哈希表，将阈值和容量设置为默认值。

元素迁移

计算完阈值和容量后，从31行开始，遍历当哈希表，rehash所有元素。如果当前位置的元素不为null，那么将哈希表上当前位置置为null，然后处理这个元素，会有3种情况：普通元素（next指针位null）、红黑树元素、链表的头节点。如果是普通元素，就是重新计算此元素在新哈希表上的位置，并放置这个元素；如果是红黑树元素，那么调用split方法rehash。

处理链表

从代码第39行开始，是元素为链表头节点的情况，先是声明了类似头尾指针的东西，然后遍历链表上的每一个元素，计算e.hash & oldCap是否为0做了不同处理。e.hash & oldCap代表什么呢？
首先由上一步我们知道，每次扩容后的哈希表容量（newCap）都是扩容前（oldCap）的2倍，并且都是2的指数幂。我们根据hash计算元素在哈希表上的索引位置时是通过(cap - 1) & hash计算的。假设扩容前的容量为16，即oldCap=16，则扩容后的容量为16*2=32。我们现在处理的是链表，那么必然是两个元素的hash值不同，但是计算哈希表位置后发生了冲突，因此就有了如下图的情况：

计算1和计算2分别是扩容前发生冲突的两个元素和扩容后这两个元素的哈希表位置的情况。可以看到，扩容后元素的索引位置只取决于元素hash值倒数第5位的值，哈希表元素扩了2倍就相当于参与hash值寻址计算的掩码大了1位。由此就可以通过e.hash & oldCap（也就是计算3）是否等于0得出元素扩容后的索引位置是应该保持不变还是等于 <原索引位置+原容量> 。通过这种方法，HashMap在对链表扩容时，不需要重新计算元素的索引位置，而是通过计算e.hash & oldCap是否为0，采用队尾插入法（这样可以保证顺序，也是JDK8的一个优化）将链表拆分为了Node<K,V> loHead（索引位置不变）和Node<K,V> hiHead（原索引位置+原容量）两个链表。

常见问题

看完上面的内容，再碰到一些常见的面试题，就很好解答了。

为什么HashMap 哈希表长度总是2的n次幂？

为了提高性能，CPU计算与运算比取模运算快。根据公式$h \mod 2^n = h \& (2^n - 1)$，可以将取模运算转化为与运算。

为什么当链表过深时，使用红黑树而不是二叉检索树或者平衡二叉树（AVL）？

二叉检索树只维护了节点间的顺序，因此在特殊情况时会出现二叉检索树退化为链表的情况。为了解决这个问题，又出现了2个变种，AVL 树（平衡二叉树）和红黑树。它们本质上都是二叉检索树，但它们都在保证左右子树差距不要太大上做了特殊的处理，保证了检索效率。
之所以选择红黑树而不是AVL树的原因是，红黑树被称为弱AVL树，牺牲了严格的高度平衡的优越条件为代价（根节点到叶子节点的距离最长不会是最短的两倍即可），同时由于红黑树的设计，任何不平衡都会在三次旋转之内解决。相比于AVL树来说，红黑树没有AVL树那么平衡，但是可以保证O(log2 n)的检索效率的同时，维护平衡性的成本更低，所以在HashMap这种需要频繁插入和删除的场景中，红黑树更合适。

HashMap加载因子为什么是0.75？转化红黑树阈值为8？

这个问题，我个人觉得多少有些卷了。。。 其实在源码中这几个参数的取值，注释中都有说明，更多的是统计学上的东西。
这两个值是相辅相成，先说加载因子，加载因子衡量的是一个散列表的空间的使用程度，加载因子越大，对空间的利用更充分，然而后果是发生冲突的几率变高，查找效率的降低。那为啥是0.75呢？其实这个并没有一个统一的结论，目前不同语言的 defaultLoadFactor 并不一样，比如 Java 是 0.75，Go 中是 0.65，Dart 中是0.8，python 中是0.762。Stackoverflow上有一个推理的思路，感兴趣的可以看一看。
转化红黑树阈值为什么是8，这个其实是基于defaultLoadFactor = 0.75这个设定的。根据源代码中的注释说明：红黑树节点占用的存储空间是普通节点的2倍，因此JDK8增加了红黑树的实现只是为了在冲突非常多的时候保证HashMap的查询效率。实际上，如果hashcode的分布不是特别特殊的情况下，转化为红黑树的机会不应该是特别大的。为了较少转化为红黑树的可能性，就需要知道桶中元素个数和其对应的概率是怎样的并选择一个概率较低的值作为阈值。由于桶中元素个数的概率分布满足泊松分布，根据计算，元素个数达到8的概率为0.00000006，足够小，因此转化红黑树的阈值就设置为了8。要注意，这个计算过程，defaultLoadFactor = 0.75是作为参数代入得，所以如果defaultLoadFactor发生了改变，那么转化红黑树的阈值可能也就需要跟着改变了。

参考

• HashMap的加载因子为什么是0.75？
• 周末我把HashMap源码又过了一遍
• HashMap加载因子为什么是0.75？转化红黑树阈值为8？